MATEMÁTICA INTRODUTÓRIA
A raiz da equação
é:
-4
4
3
5
6
A expressão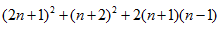 
é igual a:
7n² + 8n + 3
7n² + 8n + 4
7n² + 6n + 3
7n² + 6n + 4
7n² + 8n + 7
2 - a
a
1
0
2 + a
Dada a expressão:
2 x + 3 y para x = 5 e y = – 5
Seu valor numérico é:
0
-20
-10
-5
-2
Um engenheiro preocupado com a quantidade de senhas que precisa usar em seu cotidiano decide criar uma expressão numérica para ajuda-lo a recordar cada um dos números de suas senhas. A senha de sua rede wifi, por exemplo, começa com o número que é dado pela expressão numérica:
Esse número é:
443
700
25
899
30
Em setembro, um pedreiro comprou uma quantidade tijolos para uma construção. Em outubro ele comprou um quinto do que comprou em setembro. Em novembro, ele comprou metade do que ele comprou em setembro. Ao verificar todo o seu estoque de tijolos ele contou 4.505 tijolos. A quantidade de tijolos que o pedreiro comprou em outubro é:
1 350 tijolos.
2 650 tijolos.
5 300 tijolos.
265 tijolos.
530 tijolos.
Considerando os polinômios A = x – 2, B = 2x + 1 e C = x, o valor mais simplificado para a expressão A² - B + C é igual a:
x – 5
x2 – x – 3
x2 – 5x + 3
x2 – x – 5
x3 – x2 – 5x + 2
Sendo:
A = 6x² - 11x - 11
B = 3x + 2
Então, o quociente de A por B e o resto da divisão são, respectivamente:
-4
4
3
5
6
A expressão 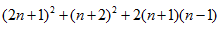é igual a:
7n² + 8n + 3
7n² + 8n + 4
7n² + 6n + 3
7n² + 6n + 4
7n² + 8n + 7
2 - a
a
1
0
2 + a
Dada a expressão:
2 x + 3 y para x = 5 e y = – 5
Seu valor numérico é:
0
-20
-10
-5
-2
Um engenheiro preocupado com a quantidade de senhas que precisa usar em seu cotidiano decide criar uma expressão numérica para ajuda-lo a recordar cada um dos números de suas senhas. A senha de sua rede wifi, por exemplo, começa com o número que é dado pela expressão numérica:
Esse número é:
443
700
25
899
30
Em setembro, um pedreiro comprou uma quantidade tijolos para uma construção. Em outubro ele comprou um quinto do que comprou em setembro. Em novembro, ele comprou metade do que ele comprou em setembro. Ao verificar todo o seu estoque de tijolos ele contou 4.505 tijolos. A quantidade de tijolos que o pedreiro comprou em outubro é:
1 350 tijolos.
2 650 tijolos.
5 300 tijolos.
265 tijolos.
530 tijolos.
Considerando os polinômios A = x – 2, B = 2x + 1 e C = x, o valor mais simplificado para a expressão A² - B + C é igual a:
x – 5
x2 – x – 3
x2 – 5x + 3
x2 – x – 5
x3 – x2 – 5x + 2
Sendo:
A = 6x² - 11x - 11
B = 3x + 2
Então, o quociente de A por B e o resto da divisão são, respectivamente:
é igual a:7n² + 8n + 3
7n² + 8n + 4
7n² + 6n + 3
7n² + 6n + 4
7n² + 8n + 7
2 - a
a
1
0
2 + a
Dada a expressão:
2 x + 3 y para x = 5 e y = – 5
Seu valor numérico é:
0
-20
-10
-5
-2
Um engenheiro preocupado com a quantidade de senhas que precisa usar em seu cotidiano decide criar uma expressão numérica para ajuda-lo a recordar cada um dos números de suas senhas. A senha de sua rede wifi, por exemplo, começa com o número que é dado pela expressão numérica:
Esse número é:
443
700
25
899
30
Em setembro, um pedreiro comprou uma quantidade tijolos para uma construção. Em outubro ele comprou um quinto do que comprou em setembro. Em novembro, ele comprou metade do que ele comprou em setembro. Ao verificar todo o seu estoque de tijolos ele contou 4.505 tijolos. A quantidade de tijolos que o pedreiro comprou em outubro é:
1 350 tijolos.
2 650 tijolos.
5 300 tijolos.
265 tijolos.
530 tijolos.
Considerando os polinômios A = x – 2, B = 2x + 1 e C = x, o valor mais simplificado para a expressão A² - B + C é igual a:
x – 5
x2 – x – 3
x2 – 5x + 3
x2 – x – 5
x3 – x2 – 5x + 2
Sendo:
A = 6x² - 11x - 11
B = 3x + 2
Então, o quociente de A por B e o resto da divisão são, respectivamente:
2 - a
a
1
0
2 + a
Dada a expressão:
2 x + 3 y para x = 5 e y = – 5
Seu valor numérico é:
0
-20
-10
-5
-2
Um engenheiro preocupado com a quantidade de senhas que precisa usar em seu cotidiano decide criar uma expressão numérica para ajuda-lo a recordar cada um dos números de suas senhas. A senha de sua rede wifi, por exemplo, começa com o número que é dado pela expressão numérica:
Esse número é:
443
700
25
899
30
Em setembro, um pedreiro comprou uma quantidade tijolos para uma construção. Em outubro ele comprou um quinto do que comprou em setembro. Em novembro, ele comprou metade do que ele comprou em setembro. Ao verificar todo o seu estoque de tijolos ele contou 4.505 tijolos. A quantidade de tijolos que o pedreiro comprou em outubro é:
1 350 tijolos.
2 650 tijolos.
5 300 tijolos.
265 tijolos.
530 tijolos.
Considerando os polinômios A = x – 2, B = 2x + 1 e C = x, o valor mais simplificado para a expressão A² - B + C é igual a:
x – 5
x2 – x – 3
x2 – 5x + 3
x2 – x – 5
x3 – x2 – 5x + 2
Sendo:
A = 6x² - 11x - 11
B = 3x + 2
Então, o quociente de A por B e o resto da divisão são, respectivamente:
0
-20
-10
-5
-2
Um engenheiro preocupado com a quantidade de senhas que precisa usar em seu cotidiano decide criar uma expressão numérica para ajuda-lo a recordar cada um dos números de suas senhas. A senha de sua rede wifi, por exemplo, começa com o número que é dado pela expressão numérica:
Esse número é:
443
700
25
899
30
Em setembro, um pedreiro comprou uma quantidade tijolos para uma construção. Em outubro ele comprou um quinto do que comprou em setembro. Em novembro, ele comprou metade do que ele comprou em setembro. Ao verificar todo o seu estoque de tijolos ele contou 4.505 tijolos. A quantidade de tijolos que o pedreiro comprou em outubro é:
1 350 tijolos.
2 650 tijolos.
5 300 tijolos.
265 tijolos.
530 tijolos.
Considerando os polinômios A = x – 2, B = 2x + 1 e C = x, o valor mais simplificado para a expressão A² - B + C é igual a:
x – 5
x2 – x – 3
x2 – 5x + 3
x2 – x – 5
x3 – x2 – 5x + 2
Sendo:
A = 6x² - 11x - 11
B = 3x + 2
Então, o quociente de A por B e o resto da divisão são, respectivamente:
443
700
25
899
30
Em setembro, um pedreiro comprou uma quantidade tijolos para uma construção. Em outubro ele comprou um quinto do que comprou em setembro. Em novembro, ele comprou metade do que ele comprou em setembro. Ao verificar todo o seu estoque de tijolos ele contou 4.505 tijolos. A quantidade de tijolos que o pedreiro comprou em outubro é:
1 350 tijolos.
2 650 tijolos.
5 300 tijolos.
265 tijolos.
530 tijolos.
Considerando os polinômios A = x – 2, B = 2x + 1 e C = x, o valor mais simplificado para a expressão A² - B + C é igual a:
x – 5
x2 – x – 3
x2 – 5x + 3
x2 – x – 5
x3 – x2 – 5x + 2
Sendo:
A = 6x² - 11x - 11
B = 3x + 2
Então, o quociente de A por B e o resto da divisão são, respectivamente:
1 350 tijolos.
2 650 tijolos.
5 300 tijolos.
265 tijolos.
530 tijolos.
Considerando os polinômios A = x – 2, B = 2x + 1 e C = x, o valor mais simplificado para a expressão A² - B + C é igual a:
x – 5
x2 – x – 3
x2 – 5x + 3
x2 – x – 5
x3 – x2 – 5x + 2
Sendo:
A = 6x² - 11x - 11
B = 3x + 2
Então, o quociente de A por B e o resto da divisão são, respectivamente:
x – 5
x2 – x – 3
x2 – 5x + 3
x2 – x – 5
x3 – x2 – 5x + 2
